Contributed by Sylvain Gravel
Hydro-Québec
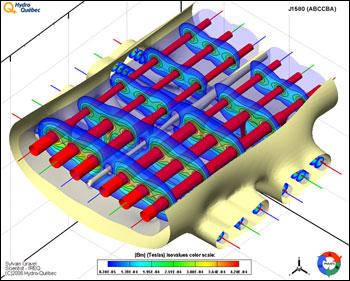
Figure 1: Magnetic flux density isosurfaces and contours near a complex configuration of distribution power lines. Phases A, B, C (0°, -120° and 120°) are represented by red, green and blue conductors respectively.
The Challenge:
Accurately Visualizing Magnetic Flux Density
In working with electrical power production and distribution, a key problem faced is being able to see the unseen – in other words, how does one view invisible electrical and magnetic forces at play?
Hydro-Québec needed to be able to see magnetic flux density near a distribution power line, which is essentially understanding the power flow in the power lines. The physical problem, having no rotational symmetry or linear periodicity, had to be solved completely in 3D.
The Researcher
Hydro-Québec is the provincial government-owned electrical power utility in Québec, Canada. The Institute of Research (IREQ) is the research facility of Hydro-Québec and one of the world’s largest laboratories studying techniques and equipment used in electrical power production, transmission, distribution, and use.
Hydro-Québec’s high-voltage Transmission and Distribution divisions as well as external partners and clients are the main beneficiaries of the research conducted at IREQ.
Sylvain Gravel is a research scientist at IREQ. Gravel, a theoretical physicist, has worked at IREQ since 1980, first as a graduate student and later as a full-time researcher. Over the years Gravel has been involved in modeling and simulation of physical phenomena related to lightning, electric fields in dielectrics, thermonuclear fusion (tokamak), hybrid vehicle dynamics, high-efficiency in-wheel motors, astrodynamics, HV lines de-icing and computational electromagnetics.
Gravel used Tecplot 360 software to create these plots illustrating the magnetic flux density isosurfaces near a dual-circuit distribution power line with two lateral secondary branching circuits.
The Solution: Utilize 3D visualization to overcome the lack of rotational symmetry
Figure 1 (above) shows a few isosurfaces of magnetic flux density (Bm), also sometimes called magnetic induction, near a complex configuration of 3-phase distribution power lines. This equally loaded dual-circuit, 3-phase 60Hz power line has two lateral branching circuits. Each 3-phase secondary branching circuit carries 20% of the main current. The main conductors and the corresponding branching conductors are connected by jumper cables. The lines were assumed balanced (no neutral currents).
Gravel explains how the data was generated: Because this is an open boundary problem, using a boundary element method (BEM) instead of finite elements eliminated the need to mesh a large volume of space far from the region of interest.” He adds that “BEM software solves Maxwell’s equations in integral form using an equivalent source Green’s function approach so computational elements need only to be defined on the surfaces of interest and not inside of them.”
Gravel computed the magnetic flux density values in 3D using Faraday, a 3D magnetic induction BEM simulation program developed by Integrated Engineering Software.
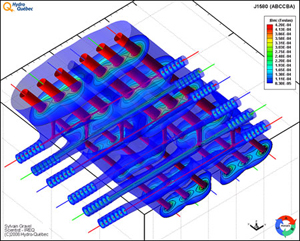
Figure 2: This plot represents the same physical situation seen from below. To show Bm around jumper cables and secondary conductors, the beige (41,5µT) isosurface was removed completely.
The fields (Bx, By, Bz and Bm and corresponding phase angles) were computed using Faraday for the given currents. A cubic region of interest (3m x 3m x 3m) was defined, field values were computed in this region on a 101 x 101 x 101 regular grid and results were exported to a 200+ MB text file.
This data was then imported into Tecplot 360. Another small input file with simple Tecplot primitives was used to create zones for the rectilinear conductors with proper phase color coding.
Then a set (C1) of contours levels for some Bm values of interest (41,5µT, 83,0µT and 420,0µT) were defined to be used for plotting the isosurfaces (respectively shown in beige, blue and red).
Transparency was added to the blue one and Value Blanking was defined above a certain value of Z for the beige isosurface to create the “open box” look and enable a view of the inner structure.
Another more complete set of contour levels (C2) between 83µT and 420µT was defined with a Cutoff Color Below value of 83µT. These levels were used to create the contour plots with flooding and lines. These were plotted on Slices parallel to the YZ and XZ planes defined at specific values of X and Y respectively, making use of the slices grouping options. Transparency was added to all the contour plots.
Titles, legend, company logo and other elements were added on the same frame and the final output was saved to a compact PNG file, which can be easily integrated in publications and presentations.
Tecplot Helps Researchers “See” Current Flow
The features of interest are the isosurfaces at 83µT (blue, transparent) and 420µT (red, solid) and, more specifically, their shape and exact position and extent in space in relation to the conductors. The contours plotted on the slices give a general idea of the magnetic flux density distribution.
At the current level used, the surfaces at Bm=420µT around each conductor can be considered independent from each other. This is not the case at 83µT where isosurfaces overlap and merge. This would also not be the case if the main currents were increased substantially.
Gravel explains, “Due to the reverse phasing (ABCCBA) of the main conductors, we have a low-field region between the two central conductors as expected. This region is the hollow cylindrical surface running between the phase C main conductors (shown in blue). This is useful as a quick check of the proper phasing of the input data.”
According to Gravel, another easily predictable but nevertheless interesting effect well shown here is the narrowing of the 420µT (red) iso-surfaces around each main conductor after each branching circuit. “The current source (100%) is assumed to be located near the observer so as each secondary circuit carries 20% of the main current, the smaller remaining current in the main conductors makes the Bm iso-surfaces shrink around them. No surprise here, of course, but it’s another good verification that nothing is seriously wrong with the results” says Gravel.
Tecplot at Work
Gravel uses Tecplot 360 almost exclusively for its 3D capabilities, iso-surfaces, 3D contouring, slicing planes and 3D arrow plots on zone geometries and mainly for electric, magnetic and thermal simulations. He also uses the software to create animations of certain physical parameters to get a better understanding of their dynamics.
Gravel adds, “These 3D views and animations can also now be incorporated in 3D PDF documents and be interactively manipulated by the final reader of the document. This adds tremendous power and versatility to Tecplot outputs.”
Researchers at IREQ use Tecplot at the research stage to explore data and reveal relations between parameters. Gravel clarifies, “About 80% of all the plots generated-although of publication quality-don’t end up in final documents but are used during this analysis phase.”
The final plots are incorporated in internal and external technical publications and reports. “Because of their powerful 3D visualization qualities,” Gravel adds, “they are also very useful for presentations to less technical audiences.”
Gravel, who has used Tecplot for 10 years, believes that Tecplot would have helped him during his days as a student. “I wish I could have had access to a 3D tool such as Tecplot when I was a student. Powerful 3D visualization can greatly enhance one’s understanding of complex physical phenomena and Tecplot is a fantastic tool for intricate what-if data exploratory work.”
Today, Tecplot facilitates Gravel’s research efforts by helping him explore data dependencies and visualize complex interactions between parameters in 3D. “Newer and better simulation and visualization tools such as Tecplot assist us with the periodic reassessment and refinement of our equipment and practices and help us remain an environment-friendly utility company,” says Gravel.
Gravel adds that it is also very useful for rapidly spotting input data errors and is also very useful for dissemination of 3D results in internal and external publications, reports and presentations.
Gravel, who has used many other technical plotting and visualization packages in the past, believes that Tecplot distinguishes itself in many ways. “Tecplot gives me more control over the details of my plots and allows me to combine several types of data representation in the same multi-variable 3D plot,” says Gravel. “Tecplot 360 doesn’t try to substitute itself for more sophisticated data analysis or simulation software; it stays focused on its primary purpose: generating advanced 3D plots, and it does it better than the other packages I have used in the past.”




