One of the most memorable parts of my finite-elements class in graduate school was a comparison of linear elements and higher-order elements for the structural analysis of a dam. As I remember, they were able to duplicate the results obtained with 34 linear elements by using a SINGLE high-order element. This made a big impression on me, but the skills I learned at that time remained largely unused until recently.
You see, my Ph.D. research and later work was using finite-volume CFD codes to solve the steady-state viscous flow. For steady flows, there didn’t seem to be much advantage to using higher than 2nd or 3rd order accuracy.
Increasing Usage of Higher-Order Methods
This has changed recently as the analysis of unsteady vortical flows have become more common. The use of higher-order (greater than second order) computational fluid dynamics (CFD) methods is increasing. Popular government and academic CFD codes such as FUN3D, KESTREL, and SU2 have released, or are planning to release, versions that include higher-order methods. This is because higher-order accurate methods offer the potential for better accuracy and stability, especially for unsteady flows. This trend is likely to continue.
CFD 2030 Vision
Commercial visual analysis codes are not yet providing full support for higher-order solutions. The CFD 2030 vision states
“…higher-order methods will likely increase in utilization during this time frame, although currently the ability to visualize results from higher order simulations is highly inadequate. Thus, software and hardware methods to handle data input/output (I/O), memory, and storage for these simulations (including higher-order methods) on emerging HPC systems must improve. Likewise, effective CFD visualization software algorithms and innovative information presentation (e.g., virtual reality) are also lacking.”
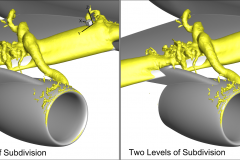
The isosurface algorithm described in this paper is the first step toward improving higher-order element visualization in the commercial visualization code Tecplot 360.
Higher-Order Finite-Element Techniques
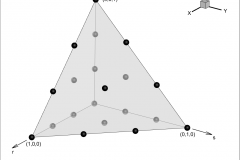
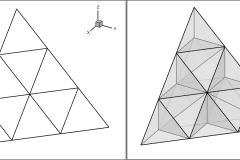
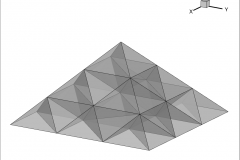
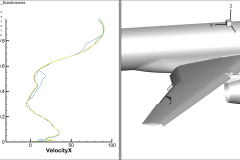
Higher-order methods can be based on either finite-difference methods or finite-element methods. While some popular codes use higher-order finite-difference methods (OVERFLOW, for example), this paper will focus on higher-order finite-element techniques. Specifically, we will present a memory-efficient recursive subdivision algorithm for visualizing the isosurface of higher-order element solutions.
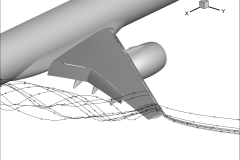
In previous papers we demonstrated this technique for quadratic tetrahedral, hexahedral, pyramid, and prism elements with Lagrangian polynomial basis functions. In this paper Optimized Implementation of Recursive Sub-Division Technique for Higher-Order Finite-Element Isosurface and Streamline Visualization we discuss the integration of these techniques into the engine of the commercial visualization code Tecplot 360 and discuss speed optimizations. We also discuss the extension of the recursive subdivision algorithm to cubic tetrahedral and pyramid elements, and quartic tetrahedral elements. Finally, we discuss the extension of the recursive subdivision algorithm to the computation of streamlines.